ESRUDIANTES SE RELIZA EL MONTAJE DE LA TEORIA DE LA NUEVA TEMATICA
REALIZAR EL RESUMEN DE LAS TEMATICAS AQUI PLANTEADAS Y REALIZAR LOS ESQUEMAS PRACTICOS
PROPIEDADES DE LA MATERIA
Todo lo que nos rodea y que sabemos como es se le llama materia. Aquello que existe pero no sabemos como es se le llama no-materia o antimateria.
Al observar la materia nos damos cuenta que existen muchas clases de ella porque la materia tiene propiedades generales y propiedades particulares.
Propiedades generales O EXTRINSECAS
Las propiedades generales son aquellas que presentan características iguales para todo tipo de materia. Dentro de las propiedades generales tenemos:
Masa
Es la cantidad de materia que posee un cuerpo.
Peso =
Es la fuerza de atracción llamada gravedad que ejerce la tierra sobre la materia para llevarla hacia su centro.
Extensión =
Es la propiedad que tienen los cuerpos de ocupar un lugar determinado en el espacio.
Impenetrabilidad =
Es la propiedad que dice que dos cuerpos no ocupan el mismo tiempo o el mismo espacio.
Inercia
Es la propiedad que indica que todo cuerpo va a permanecer en estado de reposo o movimiento mientras no exista una fuerza externa que cambie dicho estado de reposo o movimiento.
Porosidad
Es la propiedad que dice que como la materia esta constituida por moléculas entre ellas hay un espacio que se llama poro.
Elasticidad =
Es la propiedad que indica que cuando a un cuerpo se le aplica una fuerza esta se deforma y que al dejar de aplicar dicha fuerza el cuerpo recupera su forma original; lógicamente sin pasar él limite de elasticidad. "limite de influenza "
Divisibilidad =
Esta propiedad demuestra que toda la materia se puede dividir.
*
Propiedades Especificas
Todas las sustancias al formarse como materia presentan unas propiedades que las distinguen de otras y esas propiedades reciben el nombre de especificas y dichas propiedades reciben el nombre de color, olor, sabor, estado de agregación, densidad, punto de ebullición, solubilidad, etc.
El color, olor y sabor demuestra que toda la materia tiene diferentes colores, sabores u olores.
El estado de de agregación indica que la materia se puede presentar en estado sólido, liquido o gaseoso.
La densidad es la que indica que las sustancias tienen diferentes pesos y que por eso no se pueden unir fácilmente .
*
CLASIFICACIÓN DE LA MATERIA
Materia heterogéneo
Es una mezcla de sustancias en más de una fase o que son físicamente distinguibles.
EJEMPLO: mezcla de agua y aceite.
Material homogéneo:
Constituido por una sola sustancia o por varias que se encuentran en una sola fase
EJEMPLO: mezcla de sal y agua.
Solución:
Es un material homogéneo constituido por más de una sustancia. Son transparentes, estables y no producen precipitaciones. Una característica muy importante es la composición, la cual es igual en todas sus partes. Sin embargo, con los mismos componentes es posible preparar muchas otras soluciones con solo variar la proporción de aquellos
EJEMPLO: las gaseosas.
Sustancia pura:
Es un material homogéneo cuya composición química es invariable.
EJEMPLO: alcohol (etanol)
Elemento:
Sustancia conformada por una sola clase de átomos
EJEMPLO: nitrógeno gaseoso (N2), la plata (Ag)
Compuesto:
Sustancia conformada por varias clases de átomos
EJEMPLO: dióxido de carbono (CO2)
CAMBIOS DE LA MATERIA
Cambio físico: Cambio que sufre la materia en su estado, volumen o forma sin alterar su composición.
EJEMPLO: en la fusión del hielo, el agua pasa de estado sólido a líquido, pero su composición permanece inalterada.
Cambio químico: Cambio en la naturaleza de la materia, variación en su composición
EJEMPLO: en la combustión de una hoja de papel, se genera CO, CO2 y H2O a partir de celulosa, cambiando la composición de la sustancia inicial.
Cambios de estado: El estado en que se encuentre un material depende de las condiciones de presión y temperatura, modificando una de éstas variables o ambas, se puede pasar la materia de un estado a otro.
Sólido, liquido, gaseoso o plasma
CAMBIOS DE ESTADO
CARACTERÍSTICAS DE LOS DIFERENTES ESTADOS DE LA MATERIA
SÓLIDOS
LÍQUIDOS
GASES
COMPRESIBILIDAD
No se pueden comprimir
No se pueden comprimir
Sí pueden comprimirse
VOLUMEN
No se adaptan al volumen del recipiente
Se adaptan al volumen del recipiente
Se adaptan al volumen del recipiente
GRADOS DE LIBERTAD
Vibración
Vibración, rotación
Vibración, rotación, traslación
EXPANSIBILIDAD
No se expanden
No se expanden
Sí se expanden
*
REPRESENTACIÓN DE LOS COMPUESTOS
Símbolo : es la letra o letras que se emplean para representar elementos químicos. EJEMPLO: Al (aluminio)
Molécula : se forman por enlaces químicos de dos o más átomos y siempre en proporciones definidas y constantes. Son la estructura fundamental de un compuesto.
Fórmula:
Fórmula química
Fórmula empírica o mínima
Fórmula molecular
Fórmula estructural
Fórmula de Lewis o electrónica:
Es la representación de un compuesto e indica la clase y la cantidad de átomos que forman una molécula.
Está constituido por el símbolo de cada elemento presente en la sustancia, seguido por un subíndice que índica el número relativo de átomos.
Informa sobre el tipo de átomos que forman la molécula y la relación mínima en la cual estos se combinan. Expresa la composición real de un compuesto, indicando el número de átomos de cada especie que forma la molécula. La fórmula molecular es un múltiplo de la empírica. Muestra el ordenamiento geométrico o posición que ocupa cada átomo dentro de la molécula.
Representa la molécula incluyendo todos los electrones de valencia de los átomos constituyentes, estén o no comprometidos en enlaces.
EJEMPLO:
Fe2O3
¿Cuantas veces has oido hablar de la materia oscura?
Pues aqui tienes la respuesta
Sino quieren leer abajo hay unos videos que lo explican
En astrofísica y cosmología física se denomina materia oscura a la materia hipotética de composición desconocida que no emite o refleja suficiente radiación electromagnética para ser observada directamente con los medios técnicos actuales pero cuya existencia puede inferirse a partir de los efectos gravitacionales que causa en la materia visible, tales como las estrellas o las galaxias, así como en las anisotropías del fondo cósmico de microondas. No se debe confundir la materia oscura con la energía oscura. De acuerdo con las observaciones actuales de estructuras mayores que una galaxia, así como la cosmología del Big Bang, la materia oscura constituye la gran mayoría de la masa en el Universo observable. Fritz Zwicky la utilizó por primera vez para declarar el fenómeno observado consistente con las observaciones de materia oscura como la velocidad rotacional de las galaxias y las velocidades orbitales de las galaxias en los cúmulos, las lentes gravitacionales de objetos de fondo por los cúmulos de galáxias así como el Cúmulo Bala (1E 0657-56) y la distribución de temperatura de gas caliente en galaxias y cúmulos de galaxias. La materia oscura también juega un papel central en la formación de estructuras y la evolución de galaxias y tiene efectos medibles en la anisotropía de la radiación de fondo de microondas. Todas estas líneas de pruebas sugieren que las galaxias, los cúmulos de galaxias y el Universo como un todo contienen mucha más materia que la que interactúa con la radiación electromagnética: lo restante es llamado "el componente de materia oscura".
La composición de la materia oscura se desconoce, pero puede incluir neutrinos ordinarios y pesados, partículas elementales recientemente postuladas como los WIMPs y los axiones, cuerpos astronómicos como las estrellas enanas y los planetas (colectivamente llamados MACHOs) y las nubes de gases no luminosos. Las pruebas actuales favorecen los modelos en que el componente primario de la materia oscura son las nuevas partículas elementales llamadas colectivamente materia oscura no bariónica.
El componente de materia oscura tiene bastante más masa que el componente "visible" del Universo.[1] En el presente, la densidad de bariones ordinarios y la radiación en el Universo se estima que son equivalentes aproximadamente a un átomo de hidrógeno por metro cúbico de espacio. Sólo aproximadamente el 5% de la densidad de energía total en el Universo (inferido de los efectos gravitacionales) se puede observar directamente. Se piensa que en torno al 23% está compuesto de materia oscura. El 72% restante se piensa que consiste de energía oscura, un componente incluso más extraño, distribuido difusamente en el espacio.[2] Alguna materia bariónica difícil de detectar realiza una contribución a la materia oscura, aunque algunos autores defienden que constituye sólo una pequeña porción.[3] [4] Aun así, hay que tener en cuenta que del 5% de materia bariónica estimada, la mitad de ella todavía no se ha encontrado, por lo que se puede considerar materia oscura bariónica: Todas las estrellas, galaxias y gas observable forman menos de la mitad de los bariones que se supone debería haber y se cree que toda esta materia puede estar distribuida en filamentos gaseosos de baja densidad formando una red por todo el universo y en cuyos nodos se encuentran los diversos cúmulos de galaxias. Recientemente (mayo 2008) el telescopio XMM-Newton de la agencia espacial europea ha encontrado pruebas de la existencia de dicha red de filamentos.[5]
La determinación de la naturaleza de esta masa ausente es uno de los problemas más importantes de la cosmología moderna y la física de partículas. Se ha puesto de manifiesto que los nombres "materia oscura" y la "energía oscura" sirven principalmente como expresiones de nuestra ignorancia, casi como los primeros mapas etiquetados como "Terra incognita".
link: http://www.videos-star.com/watch.php?video=
martes, 13 de abril de 2010
grado once SAN FRANCISCO - ESTEQUIOMETRIA
ESTUDIANTES LEER Y REALIZAR CADA EJEMPLO PASO A PASO, REALIZAR CADA UNO DE LOS PROBLEMAS DE ACUERDO A LA TEMATICA QUE SE VAYA VIENDO EN CLASE Y LAS DUDAS LAS RESPONDO EN CLASE. ANIMO Y ESFUERZO EN EL TRABAJO
Definición
Información cuantitativa de las ecuaciones ajustadas
Los coeficientes de una ecuación ajustada representan:
* el número relativo de moléculas que participan en una reacción
* el número relativo de moles participantes en dicha reacción.
Por ejemplo en la ecuación ajustada siguiente:
la producción de dos moles de agua requieren el consumo de 2 moles de H2 un mol de O2.
Por lo tanto, en esta reacción tenemos que: "2 moles de H2, 1 mol de O2 y 2 moles de H2O" son cantidades estequiométricamente equivalentes.
Estas relaciones estequiométricas, derivadas de las ecuaciones ajustadas, pueden usarse para determinar las cantidades esperadas de productos para una cantidad dada de reactivos.
Ejemplo:
¿Cuántas moles de H2O se producirán en una reacción donde tenemos 1,57 moles de O2, suponiendo que tenemos hidrógeno de sobra?
El cociente:
es la relación estequiométrica entre el H2O y el O2 de la ecuación ajustada de esta reacción.
Ejemplo:
Calcula la masa de CO2 producida al quemar 1,00 gramo de C4H10.
Para la reacción de combustión del butano (C4H10) la ecuación ajustada es:
Para ello antes que nada debemos calcular cuantas moles de butano tenemos en 100 gramos de la muestra:
de manera que, si la relación estequiométrica entre el C4H10 y el CO2 es:
por lo tanto:
Pero la pregunta pedía la determinación de la masa de CO2 producida, por ello debemos convertir los moles de CO2 en gramos (usando el peso molecular del CO2):
De manera similar podemos determinar la masa de agua producida, la masa de oxígeno consumida, etc.
Las etapas esenciales
* Ajustar la ecuación química
* Calcular el peso molecular o fórmula de cada compuesto
* Convertir las masas a moles
* Usar la ecuación química para obtener los datos necesarios
* Reconvertir las moles a masas si se requiere
Cálculos
Cálculos de moles
La ecuación ajustada muestra la proporción entre reactivos y productos en la reacción
de manera que, para cada sustancia en la ecuación se puede calcular las moles consumidas o producidas debido a la reacción.
Si conocemos los pesos moleculares, podemos usar cantidades en gramos.
Conversión de moles a gramos:
Ejemplo: N2 ¿Cuántos moles hay en 14,0 g?
PM = 14,01 x 2 = 28,02 g/mol
Cálculos de masa
Normalmente no medimos cantidades molares, pues en la mayoría de los experimentos en el laboratorio, es demasiado material. Esto, no es así cuando trabajamos en una planta química
En general mediremos gramos, o miligramos de material en el laboratorio y toneladas en el caso de plantas químicas
Los pesos moleculares y las ecuaciones químicas nos permiten usar masas o cantidades molares
Los pasos son:
* Ajustar la ecuación química
* Convertir los valores de masa a valores molares
* Usar los coeficientes de la ecuación ajustada para determinar las proporciones de reactivos y productos
* Reconvertir los valores de moles a masa.
Para la reacción:
Tenemos un exceso de HCl, de manera que está presente todo el que necesitamos y más.
Nótese que por cada Ca producimos 1 H2
1) Calculamos el número de moles de Ca que pusimos en la reacción.
2) 10 g de Ca son 0,25 moles, como tenemos 0,25 moles de Ca, únicamente se producirán 0,25 moles de H2. ¿Cuántos gramos produciremos?
gramos de H2 = moles obtenidos x peso molecular del H2 = 0,25 moles x 2,016 (g/mol) = 0,504 g
¿Cuántos g de CaCl2 se formaron? También serán 0.25 moles. Y entonces:
gramos de CaCl2 = moles obtenidos x peso molecular del CaCl2 = 0,25 moles x 110,98 (g/mol) = 27,75 g
Algunos ejercicios prácticos
Cuando se ha ajustado una ecuación, los coeficientes representan el número de cada elemento en los reactivos y en los productos. También representan el número de moléculas y de moles de reactivos y productos.
Factores para calcular Moles-Moles
Cuando una ecuación está ajustada, basta un cálculo simple para saber las moles de un reactivo necesarias para obtener el número deseado de moles de un producto. Se encuentran multiplicando las moles deseada del producto por la relación entre las moles de reactivo y las moles de producto en la ecuación ajustada. La ecuación es la siguiente:
Ejemplo:
Cual de las siguientes operaciones es correcta para calcular el número de moles de hidrógeno necesarios para producir 6 moles de NH3 según la siguiente ecuación?
a) 6 moles NH3 x 2 moles NH3 / 3 moles H2
b) 6 moles NH3 x 3 moles NH3 / 2 moles H2
c) 6 moles NH3 x 3 moles H2 / 2 moles NH3
d) 6 moles NH3 x 2 moles H2 / 3 moles NH3
En este caso, el reactivo es H2, y el producto es NH3.
La respuesta correcta es c
a) FALSA: la relación aquí es [moles de producto / moles de reactivo], pero debe ser [moles de reactivo / moles de producto].
b) FALSA: la relación aquí es [moles de producto / moles de reactivo], pero debe ser [moles de reactivo / moles de producto].
c) VERDADERA:
d) FALSA: la relación aquí es [2 moles de reactivo / 3 moles de producto], pero debe ser [3 moles de reactivo / 2 moles de producto].
Factor para Cálculos Mol-Gramos
Para encontrar la masa de producto, basta con multiplicar las moles de producto por su peso molecular en g/mol.
Ejemplo:
¿Cuál de las siguientes operaciones calcula correctamente la masa de oxígeno producida a partir de 0,25 moles de KClO3 según la siguiente ecuación?
(Pesos Atómicos: K = 39,1, Cl = 35,45, O = 16,00).
a) 0,25 moles KClO3 x 2 moles KClO3/3 moles O2 x 32 g/1 mol O2
b) 0,25 moles KClO3 x 3 moles O2/2 moles KClO3 x 32 g/1 mol O2
c) 0,25 moles KClO3 x 2 moles KClO3/3 moles O2 x 1 mol O2/32 g
d) 0,25 moles KClO3 x 3 moles O2/2 moles KClO3 x 1 mol O2/32 g
En este caso, el reactivo es KClO3, y el producto O2
La respuesta correcta es b
a) FALSA: la relación usada aquí es [moles de reactivo / moles de producto], pero debe ser moles de producto / moles de reactivo].
b) VERDADERA:
c) FALSA: la relación usada aquí es [moles de reactivo / moles de producto], pero debe ser [moles de producto / moles de reactivo]. Además, la expresión correcta para el peso molecular es g/mol, y no mol/g.
d) FALSA: el número de moles de producto se multiplica por mol/g, pero lo correcto es por g/mol.
Factor para Cálculos Gramos-Gramos
En la cuestión correspondiente a este apartado, es muy importante estar seguros de usar la relación correcta de reactivos y productos de la ecuación ajustada.
Ejemplo:
¿Cuál de las siguientes operaciones es la correcta para calcular el número de gramos de carburo de calcio (CaC2) necesarios para obtener 5,2 gramos de acetileno (C2H2)?
(Pesos Atómicos: Ca = 40,01, C = 12,01, O = 16,00, H = 1,008).
a) 5.2 g C2H2 x (1 mol C2H2/26 g C2H2) x (1 mol CaC2/1 mol C2H2) x (64.1 g CaC2/1 mol)
b) 5.2 g C2H2 x (26 g C2H2/1 mol) x (1 mol CaC2/1 mol C2H2) x (1 mol/64.1 g CaC2)
c) 5.2 g C2H2 x (1 mol/26 g C2H2) x (1 mol C2H2/1 mol CaC2) x (1 mol/64.1 g CaC2)
d) 5.2 g C2H2 x (26 g C2H2/1 mol) x (1 mol C2H2/1 mol CaC2) x (64.1 g CaC2/1 mol)
Escribiendo la ecuación en su forma estequiométricamente correcta la respuesta es a
a) forma estequiométricamente correcta.
b) forma estequiométricamente incorrecta.
c) forma estequiométricamente incorrecta.
d) forma estequiométricamente incorrecta.
Problemas de estequiometría - Moles a Moles. Ejemplo:
Calcular el número de moles de dióxido de nitrógeno (NO2) obtenidas cuando se producen 3 moles de oxígeno en la descomposición del ácido nítrico por la luz?
En esta reacción, se obtiene 1 mol de O2 y 4 moles de NO2 cuando se descompomen 4 moles de ácido nítrico. Por tanto, cuando se forman 3 moles de O2 se forman también 3 x 4 = 12 moles de NO2.
Problemas de estequiometría - Moles a Masa. Ejemplo:
¿Cuantos moles de dióxido de azufrepueden obtenerse quemando 16 gramos de azufre?
(Pesos Atómicos: S = 32,06, O = 16,00).
En esta reacción, 1 mol de S8 reacciona para dar 8 moles de SO2. Por tanto:
<
Problemas de estequiometría - Masa a Masa. Ejemplo:
¿Que masa de H2, que reacciona con exceso de O2, produce 11.91 g de H2O?
(Pesos Atómicos: H = 1,008, O = 16,00).
en esta reacción, 2 moles de H2 reaccionan para dar 2 moles de H2O. De acuerdo con la estequiometría de la reacción:
PROBLEMAS
1) En un alto horno, el mineral de hierro, Fe2O3, se convierte en hierro mediante la reacción:
Fe2O3 (s) + 3 CO (g) -----> 2 Fe (l) + 3 CO2 (g)
a) ¿Cuántos moles de monóxido de carbono se necesitan para producir 20 moles de hierro?
b) ¿Cuántos moles de CO2 se desprenden por cada 10 moles de hierro formado?
2) Carbonato de calcio se descompone por la acción del calor originando óxido de calcio y dióxido de carbono.
a) Formula la reacción que tiene lugar y ajústala.
b) Calcula qué cantidad de óxido de calcio se obtiene si se descompone totalmente una tonelada de carbonato de calcio.
3) ¿Qué cantidad de gas cloro se obtiene al tratar 80 g de dióxido de manganeso con exceso de HCl según la siguiente reacción? MnO2 + 4 HCl ---> MnCl2 + 2 H2O + Cl2
4) La sosa cáustica, NaOH, se prepara comercialmente mediante reacción del NaCO3 con cal apagada, Ca(OH)2. ¿Cuántos gramos de NaOH pueden obtenerse tratando un kilogramo de Na2CO3 con Ca(OH)2?
Nota: En la reacción química, además de NaOH, se forma CaCO3.
5) Cuando se calienta dióxido de silicio mezclado con carbono, se forma carburo de silicio (SiC) y monóxido de carbono. La ecuación de la reacción es:
SiO2 (s) + 3 C (s) -----> SiC (s) + 2 CO (g)
Si se mezclan 150 g de dióxido de silicio con exceso de carbono, ¿cuántos gramos de SiC se formarán?
9) Se tratan 4,9 g de ácido sulfúrico con cinc. En la reacción se obtiene sulfato de cinc e hidrógeno.
a) Formula y ajusta la reacción que tiene lugar.
b) Calcula la cantidad de hidrógeno desprendido.
c) Halla qué volumen ocupará ese hidrógeno en condiciones normales.
Definición
Información cuantitativa de las ecuaciones ajustadas
Los coeficientes de una ecuación ajustada representan:
* el número relativo de moléculas que participan en una reacción
* el número relativo de moles participantes en dicha reacción.
Por ejemplo en la ecuación ajustada siguiente:
la producción de dos moles de agua requieren el consumo de 2 moles de H2 un mol de O2.
Por lo tanto, en esta reacción tenemos que: "2 moles de H2, 1 mol de O2 y 2 moles de H2O" son cantidades estequiométricamente equivalentes.
Estas relaciones estequiométricas, derivadas de las ecuaciones ajustadas, pueden usarse para determinar las cantidades esperadas de productos para una cantidad dada de reactivos.
Ejemplo:
¿Cuántas moles de H2O se producirán en una reacción donde tenemos 1,57 moles de O2, suponiendo que tenemos hidrógeno de sobra?
El cociente:
es la relación estequiométrica entre el H2O y el O2 de la ecuación ajustada de esta reacción.
Ejemplo:
Calcula la masa de CO2 producida al quemar 1,00 gramo de C4H10.
Para la reacción de combustión del butano (C4H10) la ecuación ajustada es:
Para ello antes que nada debemos calcular cuantas moles de butano tenemos en 100 gramos de la muestra:
de manera que, si la relación estequiométrica entre el C4H10 y el CO2 es:
por lo tanto:
Pero la pregunta pedía la determinación de la masa de CO2 producida, por ello debemos convertir los moles de CO2 en gramos (usando el peso molecular del CO2):
De manera similar podemos determinar la masa de agua producida, la masa de oxígeno consumida, etc.
Las etapas esenciales
* Ajustar la ecuación química
* Calcular el peso molecular o fórmula de cada compuesto
* Convertir las masas a moles
* Usar la ecuación química para obtener los datos necesarios
* Reconvertir las moles a masas si se requiere
Cálculos
Cálculos de moles
La ecuación ajustada muestra la proporción entre reactivos y productos en la reacción
de manera que, para cada sustancia en la ecuación se puede calcular las moles consumidas o producidas debido a la reacción.
Si conocemos los pesos moleculares, podemos usar cantidades en gramos.
Conversión de moles a gramos:
Ejemplo: N2 ¿Cuántos moles hay en 14,0 g?
PM = 14,01 x 2 = 28,02 g/mol
Cálculos de masa
Normalmente no medimos cantidades molares, pues en la mayoría de los experimentos en el laboratorio, es demasiado material. Esto, no es así cuando trabajamos en una planta química
En general mediremos gramos, o miligramos de material en el laboratorio y toneladas en el caso de plantas químicas
Los pesos moleculares y las ecuaciones químicas nos permiten usar masas o cantidades molares
Los pasos son:
* Ajustar la ecuación química
* Convertir los valores de masa a valores molares
* Usar los coeficientes de la ecuación ajustada para determinar las proporciones de reactivos y productos
* Reconvertir los valores de moles a masa.
Para la reacción:
Tenemos un exceso de HCl, de manera que está presente todo el que necesitamos y más.
Nótese que por cada Ca producimos 1 H2
1) Calculamos el número de moles de Ca que pusimos en la reacción.
2) 10 g de Ca son 0,25 moles, como tenemos 0,25 moles de Ca, únicamente se producirán 0,25 moles de H2. ¿Cuántos gramos produciremos?
gramos de H2 = moles obtenidos x peso molecular del H2 = 0,25 moles x 2,016 (g/mol) = 0,504 g
¿Cuántos g de CaCl2 se formaron? También serán 0.25 moles. Y entonces:
gramos de CaCl2 = moles obtenidos x peso molecular del CaCl2 = 0,25 moles x 110,98 (g/mol) = 27,75 g
Algunos ejercicios prácticos
Cuando se ha ajustado una ecuación, los coeficientes representan el número de cada elemento en los reactivos y en los productos. También representan el número de moléculas y de moles de reactivos y productos.
Factores para calcular Moles-Moles
Cuando una ecuación está ajustada, basta un cálculo simple para saber las moles de un reactivo necesarias para obtener el número deseado de moles de un producto. Se encuentran multiplicando las moles deseada del producto por la relación entre las moles de reactivo y las moles de producto en la ecuación ajustada. La ecuación es la siguiente:
Ejemplo:
Cual de las siguientes operaciones es correcta para calcular el número de moles de hidrógeno necesarios para producir 6 moles de NH3 según la siguiente ecuación?
a) 6 moles NH3 x 2 moles NH3 / 3 moles H2
b) 6 moles NH3 x 3 moles NH3 / 2 moles H2
c) 6 moles NH3 x 3 moles H2 / 2 moles NH3
d) 6 moles NH3 x 2 moles H2 / 3 moles NH3
En este caso, el reactivo es H2, y el producto es NH3.
La respuesta correcta es c
a) FALSA: la relación aquí es [moles de producto / moles de reactivo], pero debe ser [moles de reactivo / moles de producto].
b) FALSA: la relación aquí es [moles de producto / moles de reactivo], pero debe ser [moles de reactivo / moles de producto].
c) VERDADERA:
d) FALSA: la relación aquí es [2 moles de reactivo / 3 moles de producto], pero debe ser [3 moles de reactivo / 2 moles de producto].
Factor para Cálculos Mol-Gramos
Para encontrar la masa de producto, basta con multiplicar las moles de producto por su peso molecular en g/mol.
Ejemplo:
¿Cuál de las siguientes operaciones calcula correctamente la masa de oxígeno producida a partir de 0,25 moles de KClO3 según la siguiente ecuación?
(Pesos Atómicos: K = 39,1, Cl = 35,45, O = 16,00).
a) 0,25 moles KClO3 x 2 moles KClO3/3 moles O2 x 32 g/1 mol O2
b) 0,25 moles KClO3 x 3 moles O2/2 moles KClO3 x 32 g/1 mol O2
c) 0,25 moles KClO3 x 2 moles KClO3/3 moles O2 x 1 mol O2/32 g
d) 0,25 moles KClO3 x 3 moles O2/2 moles KClO3 x 1 mol O2/32 g
En este caso, el reactivo es KClO3, y el producto O2
La respuesta correcta es b
a) FALSA: la relación usada aquí es [moles de reactivo / moles de producto], pero debe ser moles de producto / moles de reactivo].
b) VERDADERA:
c) FALSA: la relación usada aquí es [moles de reactivo / moles de producto], pero debe ser [moles de producto / moles de reactivo]. Además, la expresión correcta para el peso molecular es g/mol, y no mol/g.
d) FALSA: el número de moles de producto se multiplica por mol/g, pero lo correcto es por g/mol.
Factor para Cálculos Gramos-Gramos
En la cuestión correspondiente a este apartado, es muy importante estar seguros de usar la relación correcta de reactivos y productos de la ecuación ajustada.
Ejemplo:
¿Cuál de las siguientes operaciones es la correcta para calcular el número de gramos de carburo de calcio (CaC2) necesarios para obtener 5,2 gramos de acetileno (C2H2)?
(Pesos Atómicos: Ca = 40,01, C = 12,01, O = 16,00, H = 1,008).
a) 5.2 g C2H2 x (1 mol C2H2/26 g C2H2) x (1 mol CaC2/1 mol C2H2) x (64.1 g CaC2/1 mol)
b) 5.2 g C2H2 x (26 g C2H2/1 mol) x (1 mol CaC2/1 mol C2H2) x (1 mol/64.1 g CaC2)
c) 5.2 g C2H2 x (1 mol/26 g C2H2) x (1 mol C2H2/1 mol CaC2) x (1 mol/64.1 g CaC2)
d) 5.2 g C2H2 x (26 g C2H2/1 mol) x (1 mol C2H2/1 mol CaC2) x (64.1 g CaC2/1 mol)
Escribiendo la ecuación en su forma estequiométricamente correcta la respuesta es a
a) forma estequiométricamente correcta.
b) forma estequiométricamente incorrecta.
c) forma estequiométricamente incorrecta.
d) forma estequiométricamente incorrecta.
Problemas de estequiometría - Moles a Moles. Ejemplo:
Calcular el número de moles de dióxido de nitrógeno (NO2) obtenidas cuando se producen 3 moles de oxígeno en la descomposición del ácido nítrico por la luz?
En esta reacción, se obtiene 1 mol de O2 y 4 moles de NO2 cuando se descompomen 4 moles de ácido nítrico. Por tanto, cuando se forman 3 moles de O2 se forman también 3 x 4 = 12 moles de NO2.
Problemas de estequiometría - Moles a Masa. Ejemplo:
¿Cuantos moles de dióxido de azufrepueden obtenerse quemando 16 gramos de azufre?
(Pesos Atómicos: S = 32,06, O = 16,00).
En esta reacción, 1 mol de S8 reacciona para dar 8 moles de SO2. Por tanto:
<
Problemas de estequiometría - Masa a Masa. Ejemplo:
¿Que masa de H2, que reacciona con exceso de O2, produce 11.91 g de H2O?
(Pesos Atómicos: H = 1,008, O = 16,00).
en esta reacción, 2 moles de H2 reaccionan para dar 2 moles de H2O. De acuerdo con la estequiometría de la reacción:
PROBLEMAS
1) En un alto horno, el mineral de hierro, Fe2O3, se convierte en hierro mediante la reacción:
Fe2O3 (s) + 3 CO (g) -----> 2 Fe (l) + 3 CO2 (g)
a) ¿Cuántos moles de monóxido de carbono se necesitan para producir 20 moles de hierro?
b) ¿Cuántos moles de CO2 se desprenden por cada 10 moles de hierro formado?
2) Carbonato de calcio se descompone por la acción del calor originando óxido de calcio y dióxido de carbono.
a) Formula la reacción que tiene lugar y ajústala.
b) Calcula qué cantidad de óxido de calcio se obtiene si se descompone totalmente una tonelada de carbonato de calcio.
3) ¿Qué cantidad de gas cloro se obtiene al tratar 80 g de dióxido de manganeso con exceso de HCl según la siguiente reacción? MnO2 + 4 HCl ---> MnCl2 + 2 H2O + Cl2
4) La sosa cáustica, NaOH, se prepara comercialmente mediante reacción del NaCO3 con cal apagada, Ca(OH)2. ¿Cuántos gramos de NaOH pueden obtenerse tratando un kilogramo de Na2CO3 con Ca(OH)2?
Nota: En la reacción química, además de NaOH, se forma CaCO3.
5) Cuando se calienta dióxido de silicio mezclado con carbono, se forma carburo de silicio (SiC) y monóxido de carbono. La ecuación de la reacción es:
SiO2 (s) + 3 C (s) -----> SiC (s) + 2 CO (g)
Si se mezclan 150 g de dióxido de silicio con exceso de carbono, ¿cuántos gramos de SiC se formarán?
9) Se tratan 4,9 g de ácido sulfúrico con cinc. En la reacción se obtiene sulfato de cinc e hidrógeno.
a) Formula y ajusta la reacción que tiene lugar.
b) Calcula la cantidad de hidrógeno desprendido.
c) Halla qué volumen ocupará ese hidrógeno en condiciones normales.
lunes, 1 de marzo de 2010
TRANSFORMACION DE MOLES
ESTUDIANTES DE GRADO DECIMO TEMA :TEMPERATURA Y MOLES , FACTORES DE CONVERSION
ACTIVIDADES A DESARROLLAR
1. VER LOS VIDEOS
2. REALIZAR RESUMEN
3.ESTUDIARLATEORIA DE CADA TEMA Y REALIZAR LOS EJEMPLOS
4.DESARROLLAR LOS EJERCICIOS PROPUESTOS
VIDEO 1
VIDEO 2
VIDEO 3
TEORIA DEL CONCEPTO MOL
Concepto de mol. Número de Avogadro
La masa de los átomos es muy pequeña. Si se toma como ejemplo el átomo de calcio, cuyo radio es de 2 por 10-8 cm, para completar una distancia de un centímetro habría que colocar en fila unos 50.000.000 de átomos. Esto hace que sea imposible pesar los átomos de forma individual, pues la porción más pequeña que puede obtenerse en un laboratorio contiene un número muy grande de átomos. Por esto, en cualquier situación real hay que manejar cantidades enormes de átomos, lo que hace necesario disponer de una unidad para describirlas de forma adecuada.
Concepto de mol
La unidad empleada por los químicos para expresar el peso de los átomos es el equivalente a un número muy grande de partículas y recibe el nombre de mol. De acuerdo con el Sistema Internacional, el mol se define como la cantidad de sustancia que contiene tantas entidades (átomos, moléculas, iones?) como el número de átomos existentes en 0,012 kg de carbono-12 puro.
Numerosos experimentos han llevado a los químicos a deducir que:
1 mol = 6,023 × 10 a la 23 partículas
Esa cantidad, que suele redondearse a 6,023 x 10 a la 23, se denomina constante o número de Avogadro, en honor al científico italiano Amedeo Avogadro (1776-1856).
La unidad de mol se refiere a un número fijo de «entidades» cuya identidad se debe especificar, indicando si se refiere a un mol de átomos, de moléculas o de otras partículas. Así:
* El helio es monoatómico:
1 mol de He = 6,023 x 10 a la 23 átomos de He.
* El hidrógeno es diatómico:
1 mol de H2 = 1 mol = 6,023 × 10 a la 23 moléculas de H2.1 mol de H2 = 2 × 6,023 × 10 a la 23 = 12,044 x 10 a la 23 átomos de H.
Compuestos de azufre: trióxido de azufre (SO) y ácido sulfúrico (HSO).
El mol y las masas atómicas
Cualquier tipo de átomo o molécula tiene una masa característica y definida. Como el mol se define como el número de átomos que hay en 0,012 kg (12 g) de carbono-12, se entiende que la masa en gramos de un mol de átomos de un elemento es numéricamente igual al peso atómico, en unidades de masa atómica de dicho elemento. En la tabla siguiente se ilustra esta teoría con ejemplos:
>
Elemento Masa atómica Masa muestra Contiene
Aluminio (Al) 26,98 26,98 6,023 × 10 a la 23 átomos de aluminio o un mol de átomos de aluminio
Hierro (Fe) 55,85 55,85 6,023 × 10 a la 23 átomos de hierro o un mol de átomos de hierro
Oro (Au) 196,97 196,97 6,023 × 10 a la 23 átomos de oro o un mol de átomos de oro
El mol y las masas moleculares
La masa molecular de una sustancia es la suma de las masas atómicas de los elementos que intervienen en la fórmula, multiplicados cada uno por el número de veces en que se encuentra. La masa en gramos de un mol de moléculas es numéricamente igual a esa masa fórmula. En la tabla adjunta se exponen algunos ejemplos:
Compuesto Masa molar Contiene
Agua (H2O) 18,0 g 6,023 × 10 a la 23 moléculas de agua
6,023 × 10 a la 23 átomos de oxígeno
12,044 × 10 a la 23 átomos de hidrógeno
Trióxido de azufre (SO3) 80,06 g 6,023 × 10 a la 23 moléculas de trióxido de
azufre
6,022 × 1023 átomos de azufre
18,066 × 1023 átomos de oxígeno
Tricloruro de hierro (FeCl3) 162,35 g 6,023 × 10 a la 23 moléculas de tricloruro
de hierro
6,023 × 10 a la 23 átomos de hierro
18,066 × 10 a la 23 átomos de cloro
ENTRAR A ESTE ENLACE COMO DIRECCION DE INTERNET PARA VER EL CONTENIDO ALLI ESTUDIADO
http://www.scribd.com/doc/20576271/Concepto-de-mol
VER LOS EJEMPLOS Y ENTENDERLOS
EJERCICIOS PROPUESTOS
OBJETIVO.- Distinguir los conceptos de mol y de número de Avogadro para aplicarlos en la resolución de problemas.
Introducción.- El concepto de mol es uno de los más importantes en la química. Su comprensión y aplicación son básicas en la comprensión de otros temas. Es una parte fundamental del lenguaje de la química.
MOL.- Cantidad de sustancia que contiene el mismo número de unidades elementales (átomos, moléculas, iones, etc.) que el número de átomos presentes en 12 g de carbono 12.
Cuando hablamos de un mol, hablamos de un número específico de materia. Por ejemplo si decimos una docena sabemos que son 12, una centena 100 y un mol equivale a 6.023x 10 a la. Este número se conoce como Número de Avogadro y es un número tan grande que es difícil imaginarlo.
Un mol de azufre, contiene el mismo número de átomos que un mol de plata, el mismo número de átomos que un mol de calcio, y el mismo número de átomos que un mol de cualquier otro elemento.
1 MOL de un elemento = 6.023 x 10 a la 23 átomos
Si tienes una docena de canicas de vidrio y una docena de pelotas de ping-pong, el número de canicas y pelotas es el mismo, pero ¿pesan lo mismo? NO. Así pasa con las moles de átomos, son el mismo número de átomos, pero la masa depende del elemento y está dada por la masa atómica del mismo.
Para cualquier ELEMENTO:
1 MOL = 6.023 X 10 a la 23 ÁTOMOS = MASA ATÓMICA (gramos)
Ejemplos:
Moles
Átomos
Gramos
(Masa atómica)
1 mol de S
6.023 x 10 a la 23 átomos de S
32.06 g de S
1 mol de Cu
6.023 x 10 a la 23 átomos de Cu
63.55 g de Cu
1 mol de N
6.023 x 10 a la 23 átomos de N
14.01 g de N
1 mol de Hg
6.023 x 10 a la 23 átomos de Hg
200.59 g de Hg
2 moles de K
1.2044 x 10 a la 22 átomos de K
78.20 g de K
0.5 moles de P
3.0110 x 10 a la 22 átomos de P
15.485 g de P
En base a la relación que establecimos entre moles, átomos y masa atómica para cualquier elemento, podemos nosotros convertir de una otra unidad utilizando factores de conversión. Ejemplos:
¿Cuántas moles de hierro representan 25.0 g de hierro (Fe)?
Necesitamos convertir gramos de Fe a moles de Fe. Buscamos la masa atómica del Fe y vemos que es 55.85 g . Utilizamos el factor de conversión apropiado para obtener moles.
25.0 g Fe ( 1 mol
55.85 g ) = 0.448 moles Fe La unidad del dato y del denominador del factor de conversión debe ser la misma
¿Cuántos átomos de magnesio están contenidos en 5.00 g de magnesio (Mg)?
Necesitamos convertir gramos de Mg a átomos de Mg.
Para este factor de conversión necesitamos la masa atómica que es 24.31 g.
5.00 g M (1 mol 24.31 g) = 0.206 mol Mg
¿Cuál es la masa de 3.01 x 10átomos de sodio (Na)?
Utilizaremos la masa atómica del Na (22.99 g) y el factor de conversión de átomos a gramos.
3.01 x 1023 átomos Na (22.99 g 6.023 x 10 a la 23 átomos)= 1.31 x 10 a la 23 átomos Na
Masa molar de los compuestos.-
Una mol de un compuesto contiene el número de Avogadro de unidades fórmula (moléculas o iones) del mismo. Los términos peso molecular, masa molecular, peso fórmula y masa fórmula se han usado para referirse a la masa de 1 mol de un compuesto. El término de masa molar es más amplio pues se puede aplicar para todo tipo de compuestos.
A partir de la fórmula de un compuesto, podemos determinar la masa molar sumando las masas atómicas de todos los átomos de la fórmula. Si hay más de un átomo de cualquier elemento, su masa debe sumarse tantas veces como aparezca.
Ejemplos: Calcule la masa molar de los siguientes compuestos.
KOH (hidróxido de potasio)
K 1 x 39.10 = 39.10
O 1 x 16.00 = 16.00
H 1 x 1.01 = 1.01 +
56.11 g
Cu3(PO4)2 (sulfato de cobre II)
Cu 3 x 63.55 = 190.65
P 2 x 30.97 = 61.04
O 8 x 16 = 128 +
379.69 g
Al2(SO3)3 (sulfito de aluminio)
Al 2 x 26.98 = 53.96
S 3 x 32.06 = 96.18
O 9 x 16 = 144 +
294.14 g
En el caso de los compuestos también podemos establecer una relación entre moles, moléculas y masa molar.
1 MOL = 6.022 x10 MOLÉCULAS = MASA MOLAR (gramos)
Ejemplos:
¿Cuántas moles de NaOH (hidróxido de sodio) hay en 1.0 Kg de esta sustancia?
En primer lugar debemos calcular la masa molar del NaOH
Na 1 x 22.99 = 22.99
O 1 x 16.00 = 16.00
H 1 x 1.01 = 1.01 +
40.00 g
La secuencia de conversión sería:
1.00 Kg NaOH ( 1000 g
1 Kg ) = 1000 g NaOH
1000 g NaOH ( 1 mol
40.00 g )
= 25.0 mol NaOH
¿Cuál es la masa de 5.00 moles de agua?
Calculamos la masa molar del H2O.
H 2 x 1.01 = 2.02
O 1 x 16 = 16 +
18.02 g
5.00 mol H2O ( 18.02 g
1 mol ) = 90.1 g H2O
¿Cuántas moléculas de HCl (cloruro de hidrógeno) hay en 25.0 g?
Calculamos la masa molar del HCl.
H 1 x 1.01 = 1.01
Cl 1 x 35.45 = 35.45 +
36.46 g
25.0 g HCl (
6.022 x 1023 moléculas
36.46 g) = 4.13 x 10 moléculas HCl
COMPOSICIÓN PORCENTUAL
Es el porcentaje en masa de cada uno de los elementos presentes en un compuesto.
% A =
masa total del elemento A masa molar del compuesto
X 100
Ejemplo:
Calcule la composición porcentual Ni2(CO3)3 (carbonato de niquel III)
1) Calculamos la masa molar del compuesto
Ni 2 x 58.69 = 117.38
C 3 x 12.01 = 36.03
O 9 x 16 = 144 +
297.41 g
2) Calculamos el porcentaje de cada elemento.
% Ni =
117.38
297.41
x 100 = 39.47%
% C =
36.03
297.41
x 100 = 12.11%
% O =
144
297.41
x 100 = 48.42 %
Una forma de comprobar si es correcta la composición porcentual es sumar los porcentajes de cada elemento. El total de la suma debe ser igual a 100 o un valor muy cercano. Para nuestro ejemplo:
39.47 + 12.11 + 48.42 = 100
FÓRMULA EMPÍRICA Y MOLECULAR
La fórmula empírica muestra la mínima relación de números enteros de átomos presentes en un compuesto, no es la fórmula real.
La fórmula molecular muestra el número de átomos de cada elemento que constituyen un determinado compuesto. Es la fórmula real.
Dos compuestos pueden tener la misma fórmula empírica, pero no la molecular, excepto en los casos de isomería muy frecuentes en química orgánica.
Ejemplos:
Compuesto
Fórmula molecular
Fórmula empírica
Acetileno
C2H2
CH
Benceno
C6H6
CH
Formaldehído
CH2O
CH2O
Ácido acético
C2H4O2
CH2O
Glucosa
C6H12O6
CH2O
Dióxido de carbono
CO2
CO2
Hidrazina
N2H4
NH2
A partir de la composición porcentual de un compuesto, podemos calcular la fórmula empírica y la molecular de dicho compuesto.
Ejemplo:
El propileno es un hidrocarburo cuya masa molar es de 42.00 g y contiene 14.3% de H y 85.7% de C. ¿Cuál es su fórmula empírica?¿Cuál es su fórmula molecular?
PASO 1
Tomar como base 100 g del compuesto, lo cual nos permite expresar los porcentajes como gramos.
En 100 g de propileno hay
14.3 g de H
85.7 g de C
PASO 2
Convertir los gramos a moles.
14.3 g H (
1 mol de H
1.01 g H
) =14.16 mol H
85.7 g de C (1 mol de C12.01 g C) =7.14 mol C
PASO 3
Dividir cada valor obtenido en el paso 2 entre el menor de ellos. Si los números obtenidos son enteros, usarlos como subíndices para escribir la fórmula empírica. Si los valores no son enteros , se deben multiplicar por el entero más pequeño que de por resultado otro entero.
H 14.6
7.14 = 2.04 C 7.14
7.14 = 1.0
Los decimales de .0 y .9 se aproximan al entero más cercano.
FÓRMULA EMPÍRICA: CH2
PASO 4
Obtener la masa molar de la fórmula empírica y dividir, la masa real proporcionada como dato del problema entre la masa molar de la fórmula empírica. El resultado debe ser entero o muy cercano a un entero. Este número conocido "n" (unidades de fórmula empírica) se multiplica por los subíndices de la fórmula empírica para obtener la fórmula molecular.
Fórmula empírica CH2
C 1 x 12.01 = 12.01 n = 42.00
14.03 = 2.99 3
H 2 x 1.01 = 2.02 +
14.03
FÓRMULA MOLECULAR: C3H6
Para poder obtener la fórmula molecular necesitamos calcular la empírica aun cuando el problema no la pida.
Un sulfuro de hierro contiene 2.233 g de Fe y 1.926 g de S. Si la masa molar del compuesto es 208 g, ¿cuál es la fórmula molecular del compuesto?
Como en este problema los datos están expresados en gramos, se omite el primer paso y directamente pasamos al PASO 2.
2.233 g Fe ( 1 mol Fe 55.85 g Fe)
= 0.0399 0.04mol Fe
32.06 g S (1.926 g S 1 mol S ) = 0.06 mol S
PASO 3
Fe
0.04
0.04 = 1 S 0.06
0.04 = 1.5
Las fracciones de 0.5 no se pueden redondear. El número más pequeño que multiplicado por 1.5 da un entero es 2.
A continuación se muestra una tabla con los decimales y el entero por el que se deben multiplicar.
Fracción decimal
Multiplicar por
0.5
2
0.3
3
0.25
4
En este caso usaremos el número 2 el cual debe multiplicarse por los cocientes de cada elemento.
Fe 1 x 2 = 2 S 1.5 x 2 = 3
FÓRMULA EMPÍRICA: Fe2S3
PASO 4
Fe2S3
Fe 2 x 55.85 = 111.7
S 3 x 32.06 = 96.18 +
207.88 g
n = 208
207.88 =1
Como en este caso n = 1, la fórmula empírica y la molecular son iguales.
FÓRMULA MOLECULAR:Fe2S3
¿Cuál es la masa, en gramos de un átomo de azufre? ¿Y de un átomo de hierro? ¿Y de una molécula de hidrógeno? ¿Y de una de oxígeno?.
1 Calcula la masa de un mol de átomos de azufre. De un mol de átomos de hierro. De un mol de moléculas de hidrógeno. De un mol de moléculas de oxígeno.
2¿Cuántos moles serán 27 g de hidróxido de calcio? (Na(OH))
3 ¿Cuántas moléculas hay en un mg de agua? ¿Y en 0,25 moles de metano? ¿Cuántos átomos hay en cada uno de los dos casos anteriores?
4 Se tiene una mezcla de 10 g de hidrógeno y 40 g de oxígeno. Usando los datos del sistema periódico, contesta:
A. ¿Cuántos moles de hidrógeno y oxígeno tienes?
B. ¿Cuántas moléculas de agua se formarán?
C. ¿Cuántos gramos de agua se han formado?
D. Estudia si ha sobrado algún elemento y di en qué cantidad.
5 Clasifica de mayor a menor, por el número de partículas, las siguientes cantidades: 10 g de carbonato de calcio, 0,5 moles de cloruro de sodio, 28 g de hidróxido de calcio y 0,05 moles de ácido nítrico.
6 Calcula el volumen ocupado por un mol de un gas en condiciones normales (CN).
7 El carbonato de calcio puede descomponerse bajo la acción del calor en óxido de calcio (sólido) y dióxido de carbono (gas). Si descomponemos 100 g y enfriamos los productos hasta CN. ¿Cuál será el volumen obtenido de CaO y CO2?.
8 Tenemos 90 g de agua a 25º C, la calentamos hasta 223º C y a una presión de 2 atm. ¿Qué volumen ocupará cuando esté líquida y en estado gaseosa?.
9 A la temperatura y presión de 2,5 atm se produce la combustión de 180 g de butano (C4H10) cuya riqueza es de 80 %. Calcular:
A. Masa de oxígeno necesaria.
B. Volumen de CO2 obtenido en C.N.
Datos: H=1 ; C=12 ; O=16 ; R=0,082 atm·l/mol·K.
10 Se tienen 500 g de sulfato férrico. Calcular:
A. Número de moles de sulfato férrico.
B. Número de átomos de oxígeno.
Datos: Fe=56 ; O=16 ; S=32 ; NA=6,023x 10 a la 23 partículas/mol.
11 El análisis elemental de un hidrocarburo ha permitido determinar su composición centesimal: 92,31 % de C y el resto H. Calcular la fórmula molecular (verdadera) si el peso molecular del hidrocarburo es 104. Datos: C=12 ; H=1.
12 Se somete a combustión 608 g de pentano (C5H12), cuya riqueza es del 80 %. Calcular el número de moles que se obtienen de dióxido de carbono. Datos: C=12 ; H=1 ; O=16.
13 Se tiene una mezcla de 10 g de hidrógeno y 40 g de oxígeno. ¿Cuántos moles de hidrógeno y oxígeno se tiene?¿Cuántas moléculas de agua se forman?¿Cuántos gramos de agua se han formado?
14 Hallar la fórmula empírica de un compuesto cuyo análisis dio la siguiente composición centesimal: Fe=77,7 % y O=22,3 %.
ACTIVIDADES A DESARROLLAR
1. VER LOS VIDEOS
2. REALIZAR RESUMEN
3.ESTUDIARLATEORIA DE CADA TEMA Y REALIZAR LOS EJEMPLOS
4.DESARROLLAR LOS EJERCICIOS PROPUESTOS
VIDEO 1
VIDEO 2
VIDEO 3
TEORIA DEL CONCEPTO MOL
Concepto de mol. Número de Avogadro
La masa de los átomos es muy pequeña. Si se toma como ejemplo el átomo de calcio, cuyo radio es de 2 por 10-8 cm, para completar una distancia de un centímetro habría que colocar en fila unos 50.000.000 de átomos. Esto hace que sea imposible pesar los átomos de forma individual, pues la porción más pequeña que puede obtenerse en un laboratorio contiene un número muy grande de átomos. Por esto, en cualquier situación real hay que manejar cantidades enormes de átomos, lo que hace necesario disponer de una unidad para describirlas de forma adecuada.
Concepto de mol
La unidad empleada por los químicos para expresar el peso de los átomos es el equivalente a un número muy grande de partículas y recibe el nombre de mol. De acuerdo con el Sistema Internacional, el mol se define como la cantidad de sustancia que contiene tantas entidades (átomos, moléculas, iones?) como el número de átomos existentes en 0,012 kg de carbono-12 puro.
Numerosos experimentos han llevado a los químicos a deducir que:
1 mol = 6,023 × 10 a la 23 partículas
Esa cantidad, que suele redondearse a 6,023 x 10 a la 23, se denomina constante o número de Avogadro, en honor al científico italiano Amedeo Avogadro (1776-1856).
La unidad de mol se refiere a un número fijo de «entidades» cuya identidad se debe especificar, indicando si se refiere a un mol de átomos, de moléculas o de otras partículas. Así:
* El helio es monoatómico:
1 mol de He = 6,023 x 10 a la 23 átomos de He.
* El hidrógeno es diatómico:
1 mol de H2 = 1 mol = 6,023 × 10 a la 23 moléculas de H2.1 mol de H2 = 2 × 6,023 × 10 a la 23 = 12,044 x 10 a la 23 átomos de H.
Compuestos de azufre: trióxido de azufre (SO) y ácido sulfúrico (HSO).
El mol y las masas atómicas
Cualquier tipo de átomo o molécula tiene una masa característica y definida. Como el mol se define como el número de átomos que hay en 0,012 kg (12 g) de carbono-12, se entiende que la masa en gramos de un mol de átomos de un elemento es numéricamente igual al peso atómico, en unidades de masa atómica de dicho elemento. En la tabla siguiente se ilustra esta teoría con ejemplos:
>
Elemento Masa atómica Masa muestra Contiene
Aluminio (Al) 26,98 26,98 6,023 × 10 a la 23 átomos de aluminio o un mol de átomos de aluminio
Hierro (Fe) 55,85 55,85 6,023 × 10 a la 23 átomos de hierro o un mol de átomos de hierro
Oro (Au) 196,97 196,97 6,023 × 10 a la 23 átomos de oro o un mol de átomos de oro
El mol y las masas moleculares
La masa molecular de una sustancia es la suma de las masas atómicas de los elementos que intervienen en la fórmula, multiplicados cada uno por el número de veces en que se encuentra. La masa en gramos de un mol de moléculas es numéricamente igual a esa masa fórmula. En la tabla adjunta se exponen algunos ejemplos:
Compuesto Masa molar Contiene
Agua (H2O) 18,0 g 6,023 × 10 a la 23 moléculas de agua
6,023 × 10 a la 23 átomos de oxígeno
12,044 × 10 a la 23 átomos de hidrógeno
Trióxido de azufre (SO3) 80,06 g 6,023 × 10 a la 23 moléculas de trióxido de
azufre
6,022 × 1023 átomos de azufre
18,066 × 1023 átomos de oxígeno
Tricloruro de hierro (FeCl3) 162,35 g 6,023 × 10 a la 23 moléculas de tricloruro
de hierro
6,023 × 10 a la 23 átomos de hierro
18,066 × 10 a la 23 átomos de cloro
ENTRAR A ESTE ENLACE COMO DIRECCION DE INTERNET PARA VER EL CONTENIDO ALLI ESTUDIADO
http://www.scribd.com/doc/20576271/Concepto-de-mol
VER LOS EJEMPLOS Y ENTENDERLOS
EJERCICIOS PROPUESTOS
OBJETIVO.- Distinguir los conceptos de mol y de número de Avogadro para aplicarlos en la resolución de problemas.
Introducción.- El concepto de mol es uno de los más importantes en la química. Su comprensión y aplicación son básicas en la comprensión de otros temas. Es una parte fundamental del lenguaje de la química.
MOL.- Cantidad de sustancia que contiene el mismo número de unidades elementales (átomos, moléculas, iones, etc.) que el número de átomos presentes en 12 g de carbono 12.
Cuando hablamos de un mol, hablamos de un número específico de materia. Por ejemplo si decimos una docena sabemos que son 12, una centena 100 y un mol equivale a 6.023x 10 a la. Este número se conoce como Número de Avogadro y es un número tan grande que es difícil imaginarlo.
Un mol de azufre, contiene el mismo número de átomos que un mol de plata, el mismo número de átomos que un mol de calcio, y el mismo número de átomos que un mol de cualquier otro elemento.
1 MOL de un elemento = 6.023 x 10 a la 23 átomos
Si tienes una docena de canicas de vidrio y una docena de pelotas de ping-pong, el número de canicas y pelotas es el mismo, pero ¿pesan lo mismo? NO. Así pasa con las moles de átomos, son el mismo número de átomos, pero la masa depende del elemento y está dada por la masa atómica del mismo.
Para cualquier ELEMENTO:
1 MOL = 6.023 X 10 a la 23 ÁTOMOS = MASA ATÓMICA (gramos)
Ejemplos:
Moles
Átomos
Gramos
(Masa atómica)
1 mol de S
6.023 x 10 a la 23 átomos de S
32.06 g de S
1 mol de Cu
6.023 x 10 a la 23 átomos de Cu
63.55 g de Cu
1 mol de N
6.023 x 10 a la 23 átomos de N
14.01 g de N
1 mol de Hg
6.023 x 10 a la 23 átomos de Hg
200.59 g de Hg
2 moles de K
1.2044 x 10 a la 22 átomos de K
78.20 g de K
0.5 moles de P
3.0110 x 10 a la 22 átomos de P
15.485 g de P
En base a la relación que establecimos entre moles, átomos y masa atómica para cualquier elemento, podemos nosotros convertir de una otra unidad utilizando factores de conversión. Ejemplos:
¿Cuántas moles de hierro representan 25.0 g de hierro (Fe)?
Necesitamos convertir gramos de Fe a moles de Fe. Buscamos la masa atómica del Fe y vemos que es 55.85 g . Utilizamos el factor de conversión apropiado para obtener moles.
25.0 g Fe ( 1 mol
55.85 g ) = 0.448 moles Fe La unidad del dato y del denominador del factor de conversión debe ser la misma
¿Cuántos átomos de magnesio están contenidos en 5.00 g de magnesio (Mg)?
Necesitamos convertir gramos de Mg a átomos de Mg.
Para este factor de conversión necesitamos la masa atómica que es 24.31 g.
5.00 g M (1 mol 24.31 g) = 0.206 mol Mg
¿Cuál es la masa de 3.01 x 10átomos de sodio (Na)?
Utilizaremos la masa atómica del Na (22.99 g) y el factor de conversión de átomos a gramos.
3.01 x 1023 átomos Na (22.99 g 6.023 x 10 a la 23 átomos)= 1.31 x 10 a la 23 átomos Na
Masa molar de los compuestos.-
Una mol de un compuesto contiene el número de Avogadro de unidades fórmula (moléculas o iones) del mismo. Los términos peso molecular, masa molecular, peso fórmula y masa fórmula se han usado para referirse a la masa de 1 mol de un compuesto. El término de masa molar es más amplio pues se puede aplicar para todo tipo de compuestos.
A partir de la fórmula de un compuesto, podemos determinar la masa molar sumando las masas atómicas de todos los átomos de la fórmula. Si hay más de un átomo de cualquier elemento, su masa debe sumarse tantas veces como aparezca.
Ejemplos: Calcule la masa molar de los siguientes compuestos.
KOH (hidróxido de potasio)
K 1 x 39.10 = 39.10
O 1 x 16.00 = 16.00
H 1 x 1.01 = 1.01 +
56.11 g
Cu3(PO4)2 (sulfato de cobre II)
Cu 3 x 63.55 = 190.65
P 2 x 30.97 = 61.04
O 8 x 16 = 128 +
379.69 g
Al2(SO3)3 (sulfito de aluminio)
Al 2 x 26.98 = 53.96
S 3 x 32.06 = 96.18
O 9 x 16 = 144 +
294.14 g
En el caso de los compuestos también podemos establecer una relación entre moles, moléculas y masa molar.
1 MOL = 6.022 x10 MOLÉCULAS = MASA MOLAR (gramos)
Ejemplos:
¿Cuántas moles de NaOH (hidróxido de sodio) hay en 1.0 Kg de esta sustancia?
En primer lugar debemos calcular la masa molar del NaOH
Na 1 x 22.99 = 22.99
O 1 x 16.00 = 16.00
H 1 x 1.01 = 1.01 +
40.00 g
La secuencia de conversión sería:
1.00 Kg NaOH ( 1000 g
1 Kg ) = 1000 g NaOH
1000 g NaOH ( 1 mol
40.00 g )
= 25.0 mol NaOH
¿Cuál es la masa de 5.00 moles de agua?
Calculamos la masa molar del H2O.
H 2 x 1.01 = 2.02
O 1 x 16 = 16 +
18.02 g
5.00 mol H2O ( 18.02 g
1 mol ) = 90.1 g H2O
¿Cuántas moléculas de HCl (cloruro de hidrógeno) hay en 25.0 g?
Calculamos la masa molar del HCl.
H 1 x 1.01 = 1.01
Cl 1 x 35.45 = 35.45 +
36.46 g
25.0 g HCl (
6.022 x 1023 moléculas
36.46 g) = 4.13 x 10 moléculas HCl
COMPOSICIÓN PORCENTUAL
Es el porcentaje en masa de cada uno de los elementos presentes en un compuesto.
% A =
masa total del elemento A masa molar del compuesto
X 100
Ejemplo:
Calcule la composición porcentual Ni2(CO3)3 (carbonato de niquel III)
1) Calculamos la masa molar del compuesto
Ni 2 x 58.69 = 117.38
C 3 x 12.01 = 36.03
O 9 x 16 = 144 +
297.41 g
2) Calculamos el porcentaje de cada elemento.
% Ni =
117.38
297.41
x 100 = 39.47%
% C =
36.03
297.41
x 100 = 12.11%
% O =
144
297.41
x 100 = 48.42 %
Una forma de comprobar si es correcta la composición porcentual es sumar los porcentajes de cada elemento. El total de la suma debe ser igual a 100 o un valor muy cercano. Para nuestro ejemplo:
39.47 + 12.11 + 48.42 = 100
FÓRMULA EMPÍRICA Y MOLECULAR
La fórmula empírica muestra la mínima relación de números enteros de átomos presentes en un compuesto, no es la fórmula real.
La fórmula molecular muestra el número de átomos de cada elemento que constituyen un determinado compuesto. Es la fórmula real.
Dos compuestos pueden tener la misma fórmula empírica, pero no la molecular, excepto en los casos de isomería muy frecuentes en química orgánica.
Ejemplos:
Compuesto
Fórmula molecular
Fórmula empírica
Acetileno
C2H2
CH
Benceno
C6H6
CH
Formaldehído
CH2O
CH2O
Ácido acético
C2H4O2
CH2O
Glucosa
C6H12O6
CH2O
Dióxido de carbono
CO2
CO2
Hidrazina
N2H4
NH2
A partir de la composición porcentual de un compuesto, podemos calcular la fórmula empírica y la molecular de dicho compuesto.
Ejemplo:
El propileno es un hidrocarburo cuya masa molar es de 42.00 g y contiene 14.3% de H y 85.7% de C. ¿Cuál es su fórmula empírica?¿Cuál es su fórmula molecular?
PASO 1
Tomar como base 100 g del compuesto, lo cual nos permite expresar los porcentajes como gramos.
En 100 g de propileno hay
14.3 g de H
85.7 g de C
PASO 2
Convertir los gramos a moles.
14.3 g H (
1 mol de H
1.01 g H
) =14.16 mol H
85.7 g de C (1 mol de C12.01 g C) =7.14 mol C
PASO 3
Dividir cada valor obtenido en el paso 2 entre el menor de ellos. Si los números obtenidos son enteros, usarlos como subíndices para escribir la fórmula empírica. Si los valores no son enteros , se deben multiplicar por el entero más pequeño que de por resultado otro entero.
H 14.6
7.14 = 2.04 C 7.14
7.14 = 1.0
Los decimales de .0 y .9 se aproximan al entero más cercano.
FÓRMULA EMPÍRICA: CH2
PASO 4
Obtener la masa molar de la fórmula empírica y dividir, la masa real proporcionada como dato del problema entre la masa molar de la fórmula empírica. El resultado debe ser entero o muy cercano a un entero. Este número conocido "n" (unidades de fórmula empírica) se multiplica por los subíndices de la fórmula empírica para obtener la fórmula molecular.
Fórmula empírica CH2
C 1 x 12.01 = 12.01 n = 42.00
14.03 = 2.99 3
H 2 x 1.01 = 2.02 +
14.03
FÓRMULA MOLECULAR: C3H6
Para poder obtener la fórmula molecular necesitamos calcular la empírica aun cuando el problema no la pida.
Un sulfuro de hierro contiene 2.233 g de Fe y 1.926 g de S. Si la masa molar del compuesto es 208 g, ¿cuál es la fórmula molecular del compuesto?
Como en este problema los datos están expresados en gramos, se omite el primer paso y directamente pasamos al PASO 2.
2.233 g Fe ( 1 mol Fe 55.85 g Fe)
= 0.0399 0.04mol Fe
32.06 g S (1.926 g S 1 mol S ) = 0.06 mol S
PASO 3
Fe
0.04
0.04 = 1 S 0.06
0.04 = 1.5
Las fracciones de 0.5 no se pueden redondear. El número más pequeño que multiplicado por 1.5 da un entero es 2.
A continuación se muestra una tabla con los decimales y el entero por el que se deben multiplicar.
Fracción decimal
Multiplicar por
0.5
2
0.3
3
0.25
4
En este caso usaremos el número 2 el cual debe multiplicarse por los cocientes de cada elemento.
Fe 1 x 2 = 2 S 1.5 x 2 = 3
FÓRMULA EMPÍRICA: Fe2S3
PASO 4
Fe2S3
Fe 2 x 55.85 = 111.7
S 3 x 32.06 = 96.18 +
207.88 g
n = 208
207.88 =1
Como en este caso n = 1, la fórmula empírica y la molecular son iguales.
FÓRMULA MOLECULAR:Fe2S3
¿Cuál es la masa, en gramos de un átomo de azufre? ¿Y de un átomo de hierro? ¿Y de una molécula de hidrógeno? ¿Y de una de oxígeno?.
1 Calcula la masa de un mol de átomos de azufre. De un mol de átomos de hierro. De un mol de moléculas de hidrógeno. De un mol de moléculas de oxígeno.
2¿Cuántos moles serán 27 g de hidróxido de calcio? (Na(OH))
3 ¿Cuántas moléculas hay en un mg de agua? ¿Y en 0,25 moles de metano? ¿Cuántos átomos hay en cada uno de los dos casos anteriores?
4 Se tiene una mezcla de 10 g de hidrógeno y 40 g de oxígeno. Usando los datos del sistema periódico, contesta:
A. ¿Cuántos moles de hidrógeno y oxígeno tienes?
B. ¿Cuántas moléculas de agua se formarán?
C. ¿Cuántos gramos de agua se han formado?
D. Estudia si ha sobrado algún elemento y di en qué cantidad.
5 Clasifica de mayor a menor, por el número de partículas, las siguientes cantidades: 10 g de carbonato de calcio, 0,5 moles de cloruro de sodio, 28 g de hidróxido de calcio y 0,05 moles de ácido nítrico.
6 Calcula el volumen ocupado por un mol de un gas en condiciones normales (CN).
7 El carbonato de calcio puede descomponerse bajo la acción del calor en óxido de calcio (sólido) y dióxido de carbono (gas). Si descomponemos 100 g y enfriamos los productos hasta CN. ¿Cuál será el volumen obtenido de CaO y CO2?.
8 Tenemos 90 g de agua a 25º C, la calentamos hasta 223º C y a una presión de 2 atm. ¿Qué volumen ocupará cuando esté líquida y en estado gaseosa?.
9 A la temperatura y presión de 2,5 atm se produce la combustión de 180 g de butano (C4H10) cuya riqueza es de 80 %. Calcular:
A. Masa de oxígeno necesaria.
B. Volumen de CO2 obtenido en C.N.
Datos: H=1 ; C=12 ; O=16 ; R=0,082 atm·l/mol·K.
10 Se tienen 500 g de sulfato férrico. Calcular:
A. Número de moles de sulfato férrico.
B. Número de átomos de oxígeno.
Datos: Fe=56 ; O=16 ; S=32 ; NA=6,023x 10 a la 23 partículas/mol.
11 El análisis elemental de un hidrocarburo ha permitido determinar su composición centesimal: 92,31 % de C y el resto H. Calcular la fórmula molecular (verdadera) si el peso molecular del hidrocarburo es 104. Datos: C=12 ; H=1.
12 Se somete a combustión 608 g de pentano (C5H12), cuya riqueza es del 80 %. Calcular el número de moles que se obtienen de dióxido de carbono. Datos: C=12 ; H=1 ; O=16.
13 Se tiene una mezcla de 10 g de hidrógeno y 40 g de oxígeno. ¿Cuántos moles de hidrógeno y oxígeno se tiene?¿Cuántas moléculas de agua se forman?¿Cuántos gramos de agua se han formado?
14 Hallar la fórmula empírica de un compuesto cuyo análisis dio la siguiente composición centesimal: Fe=77,7 % y O=22,3 %.
ADN-GENETICA MOLECULAR
ESTUDIANTES DE PROFUNDIZACION Y GRADO NOVENO
ACTIVIDADADES A DESARROLLAR Y PRESENTAR DEL 8 AL 12 DE MARZO
1. COPIAR ESTE ENLACE COMO DIRECCION INTERNET
http://www.scribd.com/doc/6189200/ADN-Genetica-Herramientas-moleculares ENTRAR Y VER LA INFORMACION ALLI CONTENIDA Y REALIZAR RESUMEN
2. REVISAR LA TEORIA DE LAGENETICA MOLECULAR,REALIZAR UN GLOSARIO DE TERMINOS DESCONOCIDOS
3.REALIZAR LOS ESQUEMAS GRAFICOS Y ELABORAR PREGUNTAS QUE RESUELVAN DUDAS
4. VER EL VIDEO DE GENETICA PARA COMPLEMENTAR LO VISTO EN TEORIA
5. EN EL CUADERNO TENER EL CONTENIDO VISTO EN ESTA SECCION
CONCEPTO DE GEN. MECANISMOS RESPONSABLES DE SU TRANSMISIÓN Y VARIACIÓN
Un GEN se define como la unidad mínima de información genética. Dicho de otro modo,
ACTIVIDADADES A DESARROLLAR Y PRESENTAR DEL 8 AL 12 DE MARZO
1. COPIAR ESTE ENLACE COMO DIRECCION INTERNET
http://www.scribd.com/doc/6189200/ADN-Genetica-Herramientas-moleculares ENTRAR Y VER LA INFORMACION ALLI CONTENIDA Y REALIZAR RESUMEN
2. REVISAR LA TEORIA DE LAGENETICA MOLECULAR,REALIZAR UN GLOSARIO DE TERMINOS DESCONOCIDOS
3.REALIZAR LOS ESQUEMAS GRAFICOS Y ELABORAR PREGUNTAS QUE RESUELVAN DUDAS
4. VER EL VIDEO DE GENETICA PARA COMPLEMENTAR LO VISTO EN TEORIA
5. EN EL CUADERNO TENER EL CONTENIDO VISTO EN ESTA SECCION
CONCEPTO DE GEN. MECANISMOS RESPONSABLES DE SU TRANSMISIÓN Y VARIACIÓN
Un GEN se define como la unidad mínima de información genética. Dicho de otro modo,
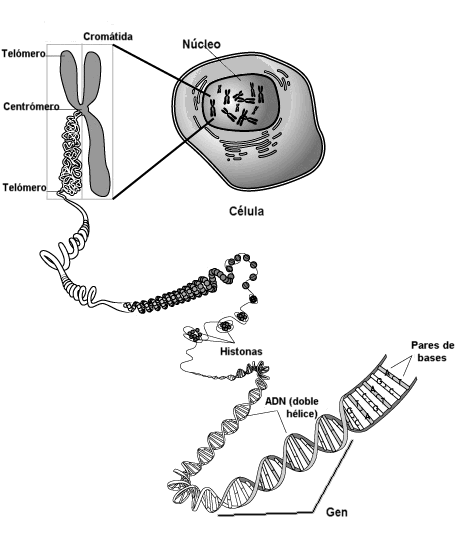
Un GEN es el fragmento más pequeño de una molécula de DNA que posee información completa para un carácter determinado
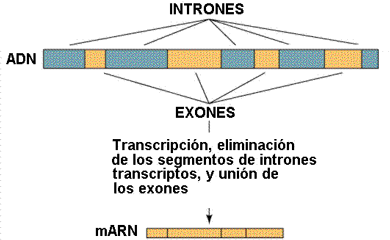
A veces el gen está formado por una secuencia de bases, pero en eucariotas es frecuente que un gen esté constituido por varios fragmentos de DNA separados por secuencias sin sentido que no codifican ninguna proteína. A las partes con sentido que sirven para fabricar la proteína se les llama EXONES, y a las partes sin sentido intercaladas en el gen INTRONES, que deben ser eliminados tras la transcripción.
Los genes se encuentran en los cromosomas. Los cromosomas pueden ser definidos como un conjunto de genes unidos o GENES LIGADOS, que son aquellos que se heredan juntos (si no se da recombinación genética).
En esencia, un gen es una secuencia de nucleótidos que codifica para una proteína determinada, según la hipótesis UN GEN = UNA ENZIMA.
Lo que heredamos de nuestros padres son, en realidad, sus genes.
Para que los genes se puedan transmitir de padres a hijos, deben poder copiarse antes de la reproducción, de manera que los padres mantienen su información a la vez que se la pasan a sus hijos a través de los gametos, durante la reproducción sexual.
Los procesos de formación de gametos (gametogénesis) y de unión de gametos de individuos diferentes en la reproducción (fecundación) se convierten así en procesos fundamentales para el mantenimiento de la especie. Estos procesos son posibles gracias a la información de los genes, y son necesarios para aumentar la variabilidad de las poblaciones, mediante la recombinación genética y el propio proceso aleatorio de fecundación, variabilidad que, junto con las mutaciones, constituirá la base de la evolución.
Cuando los genes se expresan, se desarrollan los caracteres, es decir, el fenotipo de un individuo.
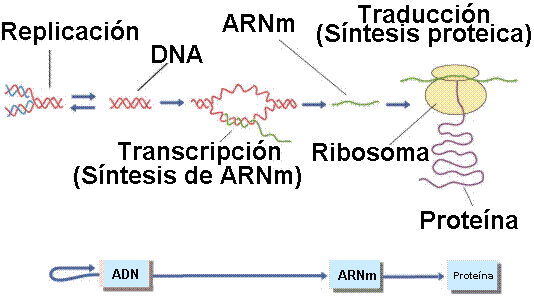
La transmisión y expresión de los genes se lleva a cabo mediante tres procesos que constituyen el "Dogma central de la Genética Molecular", que son:
- La
Replicación.- La
Transcripción.- La
Traducción.
La estructura del ADN
Erwin Chargaff analizó las base nitrogenadas del ADN en diferentes formas de vida, concluyendo que, la cantidad de purinas no siempre se encontraban en proporciones iguales a las de las pirimidinas (contrariamente a lo propuesto por Levene), la proporción era igual en todas las células de los individuos de una especie dada, pero variaba de una especie a otra.
Los experimentos de Hershey-Chase probaron que el ADN era el material genético pero, no como el ADN conformaba los genes. El ADN debía transferir información de la célula de origen a la célula hija. Debía también contener información para replicarse a si mismo, ser químicamente estable y tener pocos cambios. Sin embargo debía ser capaz de cambios mutacionales. Sin mutaciones no existiría el proceso evolutivo.
Muchos científicos se interesaron en descifrar la estructura del ADN, entre ellos, Francis Crick, James Watson, Rosalind Franklin, y Maurice Wilkins.
 |  |  |
| Maurice Wilkins (1999) | Rosalind Franklin (1920-1958) | |
 | ||
| Watson en la Conferencia de Asilomar, Estados Unidos (1979) | ||
| Watson (23 años) y Crick (34 años) Laboratorio Cavendish, Cambridge, Inglaterra circa 1953) | ||
Rosalind Franklin
A finales de la primavera de 1952, la cristalógrafa británica Rosalind Franklin (1920-1958) obtuvo una fotografía de difracción de rayos X que reveló, de manera inconfundible, la estructura helicoidal de la molécula del ADN.
| Rosalind Franklin falleció en 1958, a los 37 años, víctima de un cáncer en los ovarios. Su invaluable aportación a este descubrimiento no fue reconocida ni en vida de la cristalógrafa ni de manera póstuma, aunque poco a poco se empieza a conocer su historia. |  |
| Fotografía 51. Difracción de rayos X del ADN |
El modelo de Watson y Crick
A fines de Febrero de 1953, Rosalind Franklin, escribió en su cuaderno de notas que la estructura del ADN tenía dos cadenas, ya antes había deducido que que los grupos fosfatos se encontraban en el exterior y que el ADN existe en dos formas........
Watson y Crick eran investigadores teóricos que integraron todos los datos disponibles en su intento de desarrollar un modelo de la estructura del ADN. Los datos que se conocían por ese tiempo eran :
-
que el ADN era una molécula grande también muy larga y delgada.
-
los datos de las bases proporcionados por Chargaff (A=T y C=G; purinas/pirimidinas=k para una misma especie).
-
los datos de la difracción de los rayos-x de Franklin y Wilkins (King's College de Londres).
-
Los trabajos de Linus Pauling sobre proteínas (forma de hélice mantenida por puentes hidrógeno), quién sugirió para el ADN una estructura semejante.
| El ADN es una doble hélice, con las bases dirigidas hacia el centro, perpendiculares al eje de la molécula (como los peldaños de una escalera caracol) y las unidades azúcar-fosfato a lo largo de los lados de la hélice (como las barandas de una escalera caracol). |  |
| http://www.ncbi.nlm.nih.gov |
Las hebras que la conforman son complementarias (deducción realizada por Watson y Crick a partir de los datos de Chargaff, A se aparea con T y C con G, el apareamiento se mantiene debido a la acción de los puentes hidrogeno entre ambas bases). Tome nota que una purina con doble anillo siempre se aparea con una pirimidina con un solo anillo en su molécula.
Las purinas son la Adenina (A) y la Guanina (G). Durante este curso hablamos del Adenosin trifosfato (ATP), pero en ese caso el azúcar era la ribosa, mientras que en el ADN se encuentra la desoxirribosa.
Las Pirimidinas son la Citosina (C) y la Timina (T).
 |
| Imagen de G. S. Stent, Molecular Biology of Bacterial Viruses. Copyright © 1963 by W. H. Freeman and Company |
Las bases son complementarias, con A en un lado de la molécula únicamente encontramos T del otro lado, lo mismo ocurre con G y C. Si conocemos la secuencia de bases de una de las hebras, conocemos su complementaria.
| |
En cada extremo de una doble hélice lineal de DNA
A, el extremo 3'-OH de una de las hebras es adyacente al extremo 5'-P (fosfato) de la otra. En otras palabras, las dos hebras son antiparalelas, es decir, tienen una orientación diferente. En el esqueleto azucar -fosfato de del ADN los grupos fosfato se conectan al carbono 3´ de la molécula de desoxirribosa y al carbono 5´ de la siguiente, uniendo azúcares sucesivos. La prima (´) indica la posición del carbono en un azúcar. Por convención, la secuencia de bases de una hebra sencilla se escribe con el extremo 5'-P a la izquierda.
VIDEO No. 1
sábado, 13 de febrero de 2010
FACTORES DE CONVERSION
ESTUDIANTES GRADO NOVENO LOS SALUDO ESTE FIN DE SEMANA CON DESEOS DE PROFUNDIZAR EN LOS TEMAS VISTOS E INICIAR EL NUEVO TEMA
1. INICIO SEGUNDO TEMA: REALIZAR RESUMEN POR TITULO Y REALIZAR CUADROS DE LAS UNIDADES PARA PRESENTAR PROXIMA SEMANA
VIDEO 1
VIDEO 2 TEMA SISTEMA INTERNACIONAL DE MEDIDAS
Unidades básicas
El Sistema Internacional de Unidades consta de siete unidades básicas. Son las unidades utilizadas para expresar las magnitudes físicas definidas como básicas, a partir de las cuales se definen las demás:
Magnitud física básica Símbolo dimensional Unidad básica Símbolo de la Unidad Observaciones Longitud L metro m Se define fijando el valor de la velocidad de la luz en el vacío Tiempo T segundo s Se define fijando el valor de la frecuencia de la transición hiperfina del átomo de cesio. Masa M kilogramo kg Es la masa del «cilindro patrón» custodiado en la Oficina Internacional de Pesos y Medidas, en Sèvres (Francia). Intensidad de corriente eléctrica I amperio A Se define fijando el valor de constante magnética. Temperatura Θ kelvin K Se define fijando el valor de la temperatura termodinámica del punto triple del agua. Cantidad de sustancia N mol mol Se define fijando el valor de la masa molar del átomo de carbono-12 a 12 gramos/mol. Véase también número de Avogadro Intensidad luminosa J candela cd Véase también conceptos relacionados: lumen, lux e iluminación física Las unidades básicas tienen múltiplos y submúltiplos, que se expresan mediante prefijos. Así, por ejemplo, la expresión «kilo» indica ‘mil’ y, por lo tanto, 1 km son 1000 m, del mismo modo que «mili» indica ‘milésima’ y, por ejemplo, 1 mA es 0,001 A.
Es la única unidad básica con un prefijo multiplicativo, lo que induce a error, pues se puede interpretar que la unidad básica es el gramo. Es también la única unidad que se sigue definiendo en términos de un objeto patrón, por las dificultades que presenta definirlo mediante un experimento, de modo semejante a como se hace en las demás, aunque se han propuesto varios métodos.
Definiciones de las unidades básicas
- Definición: un metro es la longitud de trayecto recorrido en el vacío por la luz durante un tiempo de 1/299 792 458 de segundo.
- Definición: un kilogramo es una masa igual a la de un cilindro que se encuentra en la Oficina Internacional de Pesos y Medidas, en Sèvres; Francia.
- Definición: el segundo es la duración de 9 192 631 770 periodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133.
- Ampere o amperio (A). Unidad de intensidad de corriente eléctrica.
- Definición: un amperio es la intensidad de una corriente constante que manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno de otro en el vacío, produciría una fuerza igual a 2•10-7 newton por metro de longitud.
- Kelvin (K). Unidad de temperatura termodinámica.
- Definición: un kelvin es la temperatura termodinámica correspondiente a la fracción 1/273,16 de la temperatura termodinámica del punto triple del agua.
- Mol (mol). Unidad de cantidad de sustancia.
- Definición: un mol es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 0,012 kilogramos de carbono 12. Cuando se emplea el mol, es necesario especificar las unidades elementales, que pueden ser átomos, moléculas, iones, electrones u otras partículas o grupos especificados de tales partículas.
- Candela (cd). Unidad de intensidad luminosa.
- Definición: una candela es la intensidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 540•1012 hercios y cuya intensidad energética en dicha dirección es 1/683 vatios por estereorradián.
Unidades derivadas
Con esta denominación se hace referencia a las unidades utilizadas para expresar magnitudes físicas que son resultado de combinar magnitudes físicas tomadas como básicas.
El concepto no debe confundirse con los múltiplos y submúltiplos, los que son utilizados tanto en las unidades básicas como en las unidades derivadas, sino que debe relacionarse siempre a las magnitudes que se expresan. Si estas son longitud, masa, tiempo, intensidad de corriente eléctrica, temperatura, cantidad de sustancia o intensidad luminosa, se trata de una magnitud básica, y todas las demás son derivadas.
Ejemplos de unidades derivadas
- Unidad de volumen o metro cúbico, resultado de combinar tres veces la longitud, una de las magnitudes básicas.
- Unidad de densidad o cantidad de masa por unidad de volumen, resultado de combinar la masa (magnitud básica) con el volumen (magnitud derivada). Se expresa en kilogramos por metro cúbico y no tiene nombre especial.
- Unidad de fuerza, magnitud que se define a partir de la segunda ley de Newton (fuerza=masa × aceleración). La masa es una de las magnitudes básicas pero la aceleración es derivada. Por tanto, la unidad resultante (kg • m • s-2) es derivada. Esta unidad derivada tiene nombre especial, newton.[1]
- Unidad de energía, que por definición es la fuerza necesaria para mover un objeto en una distancia de un metro, es decir fuerza por distancia. Su nombre es el julio (unidad) (joule en inglés) y su símbolo es J. Por tanto, J=N • m.
En cualquier caso, siempre es posible establecer una relación entre las unidades derivadas y las básicas mediante las correspondientes ecuaciones dimensionales.
Tabla de múltiplos y submúltiplos
El separador decimal estará en línea con los dígitos y se empleara la coma (,) salvo textos en inglés que emplean el punto (.). No debe de ponerse ningún otro signo entre los números. Para facilitar la lectura se pueden agrupar números de 3 en 3 a partir de la coma decimal, separados por un espacio en blanco Ejemplo: 123 456 789,987 546. En algunos países se acostumbra a separar los miles por un punto para facilitar su lectura (Ejemplo: 123.456.789,987 546), siendo esta notación desaconsejada y ajena a la normativa establecida en el Sistema Internacional de Unidades.
1000n 10n Prefijo Símbolo Escala Corta Escala Larga Equivalencia Decimal en los Prefijos del SI Asignación 10008 1024 yotta Y Septillón Cuatrillón 1 000 000 000 000 000 000 000 000 1991 10007 1021 zetta Z Sextillón Mil trillones 1 000 000 000 000 000 000 000 1991 10006 1018 exa E Quintillón Trillón 1 000 000 000 000 000 000 1975 10005 1015 peta P Cuatrillón Mil billones 1 000 000 000 000 000 1975 10004 1012 tera T Trillón Billón 1 000 000 000 000 1960 10003 109 giga G Billón Mil millones (o millardo) 1 000 000 000 1960 10002 106 mega M Millón 1 000 000 1960 10001 103 kilo k Mil 1 000 1795 10002/3 102 hecto h Centena 100 1795 10001/3 101 deca da / D Decena 10 1795 10000 100 ninguno Unidad 1 1000−1/3 10−1 deci d Décimo 0.1 1795 1000−2/3 10−2 centi c Centésimo 0.01 1795 1000−1 10−3 mili m Milésimo 0.001 1795 1000−2 10−6 micro µ Millonésimo 0.000 001 1960 1000−3 10−9 nano n Billonésimo Milmillonésimo 0.000 000 001 1960 1000−4 10−12 pico p Trillonésimo Billonésimo 0.000 000 000 001 1960 1000−5 10−15 femto f Cuatrillonésimo Milbillonésimo 0.000 000 000 000 001 1964 1000−6 10−18 atto a Quintillonésimo Trillonésimo 0.000 000 000 000 000 001 1964 1000−7 10−21 zepto z Sextillonésimo Miltrillonésimo 0.000 000 000 000 000 000 001 1991 1000−8 10−24 yocto y Septillonésimo Cuatrillonésimo 0.000 000 000 000 000 000 000 001
1991
domingo, 7 de febrero de 2010
ESTUDIANTES DE GRADO NOVENO Y PROFUNDIZACION DE GRADO ONCE
GENÈTICA
1. realizar la lectura teórica y hacer un resumen de cada titulo
2. ver los videos y organizar en 7 diagramas (graficos, dibujos, cuadros, mapas y otros) de lo presentado en los videos para realizar sustentacion oral y/o exposicion al azar.
HERENCIA
La herencia es el parecido orgánico adquirido de los progenitores (transmisión de los caracteres de los ascendientes a los descendientes). La genética es la ciencia que se ocupa del estudio de la herencia intenta esclarecer la naturaleza del material genético transmitido a los descendientes, como se produce la transferencia de dicho material y cuales son los procesos que aseguran la realización material de los caracteres.
ASPECTO HISTORICO
Desde las civilizaciones babilónicas y sirias se sabía que los caracteres se transmiten de progenitores a descendencia. Después de Aristóteles todavía no se conocía el mecanismo de transmisión. Durante los siglos XVII y XVIII ciertos investigadores preformistas indican que el nuevo ser ya está preformado en el huevo o en los gametos. Posteriormente vieron que esto no era cierto porque al estudiar los gametos comprobaron que eran masas de protoplasma uniforme, otros indicaban que había fuerzas místicas externas que provocaban el desarrollo del huevo. Desde la edad media hasta el siglo XIX la herencia fue estudiada por criadores de animales indicando que de la unión de dos progenitores aparecían descendientes con características intermedias a los progenitores y los llamaron híbridos, sus seguidores se conocieron como hibridistas. Kolrenter estudió los rasgos de los híbridos comparándolos con los progenitores encontró que: los híbridos no siempre eran de características intermedias, que determinados rasgos desaparecían en híbridos pero aparecían en su descendencia.
MENDEL
Padre de la genética, descubrió los mecanismos básicos de la herencia, estudió la planta del guisante a través de distintos procesos: a) Selección de una variedad de línea pura para cada carácter: Roja x Roja : 100% rojab) Cruzo plantas que se diferenciaban en un carácter siendo líneas puras, Lisa x Rugosa: 100% lisa; estos a su vez se podrían cruzar dando Lisa x Lisa : 25 % rugoso y 75 % liso.c) Cruzo líneas de plantas que se diferenciaban en dos caracteres, Altas-Rojas x Pequeñas – Blancas: 100% altas y rojas; al cruzarse entre si Altas-Rojas x Altas – Rojas: altas rojas, altas blancas, pequeñas rojas, pequeñas blancas.Para explicar esto definió las unidades hereditarias que se presentan por pares y cada una será la responsable de un carácter.
Leyes de la herencia
Ley de la segregación; las unidades hereditarias existen por pares en el individuo durante la formación de los gametos estas se separan y cada una irá a un gameto, de esta forma cada gameto solo tiene un ejemplar de cada tipo.Ley de la combinación; la distribución de cada par de las unidades hereditarias es independiente de la distribución de otros pares.
Términos
Generación parenteral, es la primera generaciónF1; primera generación filialF2; segunda generación filialFenotipo, apariencia física que resulta de la actividad de un par de genes. Los dos genes que controlan un rasgo se representan por un par de letras, uno es dominante el cual enmascara la acción del recesivo.Genotipo, conjunto de todos los genes de un ser vivoIndividuo homocigoto, el que tiene los dos genes que determinan un carácterIndividuo heterocigoto, el que tiene los dos genes que determinan un carácter distintoAlelos, genes que se encuentran en oposiciónCruzamiento monohíbrido, cruzamiento en el que hay presente únicamente un par de alelosCruzamiento dihíbrido, cruzamiento en el que hay presente dos pares de alelos
Base citológica de la herencia
Las unidades hereditarias deben tener relación con los cromosomas, tras mendel se descubrió la conducta de los cromosomas durante la gametogénesis.Surge la teoría cromosómica de la herencia propuesta por Sutton (1902), los genes están en los cromosomas y se transmiten a los descendientes durante la gametogénesis.
VIDEO 2
SALUDOS ESTUDIANTES SAN PABLO APOSTOL
VER ELVIDEO Y REALIZAR RESUMEN QUE REFUERZE LO VISTO EN CLASE
VIDEO 1
VIDEO 2: OBSERVAR EL VIDEO Y REALIZAR LOS APUNTES CORRESPONDIENTES CON LOS DATOS CLAVES Y QUE SEAN NUEVOS EN EL VOCABULARIO
Suscribirse a:
Entradas (Atom)